I am interested in making a contribution to Emedded Optimal Transport by extending some of the low dimensional encoding techniques to Optimal Transport. This is the first of my projects to learn the computational literature and techniques

You can visit my code: (https://github.com/EvanMisshula/variational-encoder)

🧠 What Is a Variational Autoencoder?

A Variational Autoencoder (VAE) is a type of generative model. It learns to represent data (like images, text, etc.) using a smaller number of latent variables, and it can also generate new data that looks like the training data.

It's based on two main ideas:

1. Autoencoders – Learn to compress and then reconstruct data.
2. Variational inference – Approximate complex probability distributions using simpler ones.

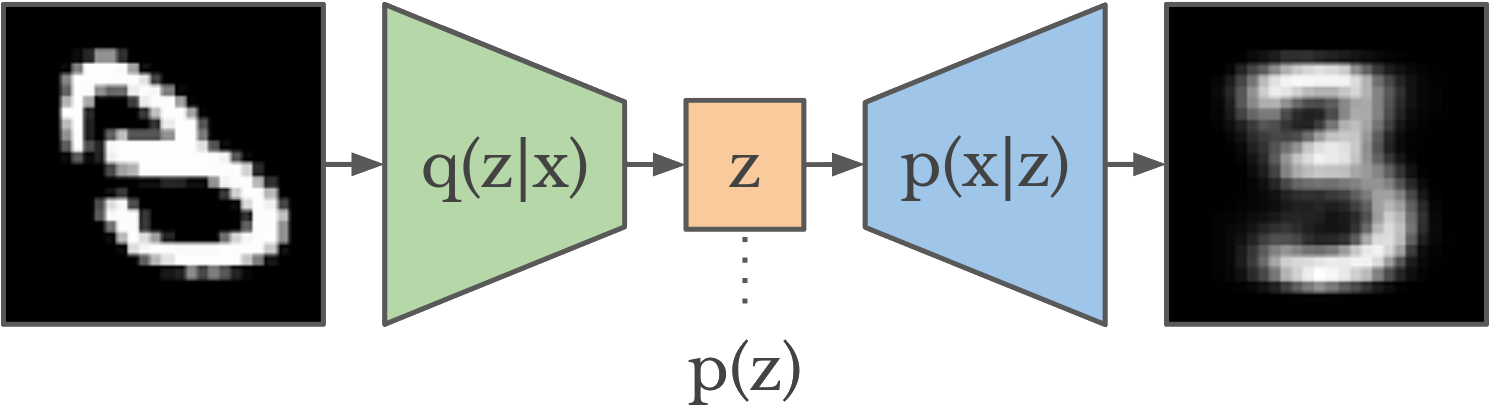
🔧 Architecture of a VAE

A VAE consists of two neural networks:

Component	Name	Description
---------	----------------------------	------------------------------------------------------------------------------------
Encoder	\( q\_{\phi(z \vert x)} \)	Takes data \(x\) and produces a distribution over latent variables \(z\).
Decoder	\( p\_{\theta(x \vert z)} \)	Takes a sample \(z\)and tries to reconstruct the original data \(x\).

Instead of mapping $x \rightarrow z \rightarrow x$ directly, the VAE treats $z$ as random and uses probability distributions.

🎯 Goal of the VAE

Learn two things:

1. How to compress data into a meaningful latent representation $z$.
2. How to generate new data from latent variables.

We want to learn the joint probability:

\begin{equation} p_\theta(x, z) = p_\theta(x|z)p(z) \end{equation}

and its marginal:

\begin{equation} p_\theta(x) = \int p_\theta(x|z) p(z) \, dz \end{equation}

But this integral is hard, so we use a trick.

The Variational Inference Trick

We approximate the true posterior $p(z|x)$ using a simpler distribution $q_\phi(z|x)$. Then we optimize the Evidence Lower Bound (ELBO):

\begin{equation} \log p_\theta(x) \geq \mathbb{E}{q\phi(z|x)}[\log p_\theta(x|z)] - \mathrm{KL}(q_\phi(z|x) \Vert p(z)) \end{equation}

Breakdown of ELBO:

• $\mathbb{E}{q\phi(z|x)}[\log p_\theta(x|z)]$ = reconstruction accuracy.
• $\mathrm{KL}(\cdot)$ = how close our approximation $q$ is to the prior $p(z)$ (usually a standard normal).

Training Procedure

1. Given input $x$, encode it to parameters $\mu(x), \sigma(x)$ for a Gaussian distribution.
2. Sample $z \sim \mathcal{N}(\mu(x), \sigma^2(x))$ using the reparameterization trick:

\begin{equation} z = \mu + \sigma \odot \epsilon, \quad \epsilon \sim \mathcal{N}(0, I) \end{equation}

1. Decode $z \rightarrow x'$ and compare to original $x$.
2. Optimize the ELBO using gradient descent.

Why Use VAEs?

1. Uncertainty-aware: Learns distributions, not just points.
2. Generative: Can sample new data points by sampling $z \sim \mathcal{N}(0, I)$.
3. Smooth latent space: Small changes in $z$ lead to smooth changes in generated $x$.
4. Principled framework: Based on variational inference and probability.

Example: MNIST Digits

The encoder maps digit images (28×28 pixels) to a 2D latent space.

The decoder learns to reconstruct digits from 2D points.

You can sample from this 2D space to generate new digit images!

Summary

Concept	Object	Description
---------------------	-----------------------------	---------------------------------------------------------------
Latent Variable	\(z\)	Hidden representation of the data
Encoder	\( q\_{\phi(z \vert x)} \)	Neural network that learns \(z\) from \(x\)
Decoder	\( p\_{\theta(x \vert z)} \)	Reconstructs or generates \(x\) from \(z\)
ELBO		A loss function that balances reconstruction and regularization
Reparameterization		Trick to make sampling differentiable for backpropagation